
Bayesian 통계와 신뢰도 분석
Summary
본 자료는 신뢰도 분석에서 실험 데이터나 필드 데이터가 이용 가능할 경우 Bayes 정리를
이용하여 신뢰도 분석을 하는 과정을 설명하였으며, 또한 간단한 예를 통하여 쉽게 이해하도록
하여 신뢰도 분석에 도움을 주고자 한다.
<제목 차례>
1. Bayesian 통계와 신뢰도 분석
2. Bayes 정리
가. Bayes 예(이산 분포)
나. Bayes 예(연속 분포)
참고자료
1. Bayesian 통계와 신뢰도 분석
18세기 영국의 수학자 Reverend Thomas Bayes는 새로운 정보가 주어짐에 따라 어떤 사상이 발생
할 확률을 결정하는 방법론을 발표하였으나, 이 이론은 1958년 학술지에 다시 소개되기까지 가치를
인정받지 못하였다. 그러나 20세기 중반 이후에 Bayesian 이론은 이전의 고전적 통계학과는 다른
새로운 분야의 통계학인 Bayesian 통계학을 확립하는 초석의 역할을 하게 되었다.
신뢰도 분석에서 Bayesian 통계에 대한 사용은 점차 늘어나고 있다. Bayesian 통계의 장점은 가용한
데이터의 조합에 근거하여 신뢰도 예측을 하기 위해 실험 데이터나 필드 데이터와 같은 최근의 정보
를 이전의 정보(예측, 테스트 결과, 공학적 판단)와 조합하여 활용할 수 있다는 것이다. 이것은 또한
더 업데이트 되어 축적된 테스트 데이터를 계속적으로 사용할 수 있다. Bayesian 통계는 공학적 설
계에도 유용하다. 왜냐하면 그것은 새로운 설계의 초기 신뢰도 예측을 하기 위해 이전에 비슷한 설
계를 했던 경험이 있는 equipment에 근거하여 공학적 판단을 내리는 것이 가능하기 때문이다.
Bayesian과 Bayesian이 아닌 접근 사이의 가장 기본적인 차이점은 전자는 현재와 그 전의 데이터를
모두 사용하는 것이고, 반면 후자는 단지 현재의 데이터만 사용한다는 것이다.
Bayesian 접근의 주된 단점 중 하나는 이전 데이터를 선택하는데 상당히 주의를 기울여야 하는 것
이다. 만약 Bayesian 분석에 대해 마구잡이 식으로 선택된 데이터가 있다면 Bayesian 분석의 결과
는 정확하지 못할 수 있다.
그러므로 Bayesian 방법을 통한 신뢰도 분석이 인정을 받으려면, 이전 데이터의 올바른 선택에 달
려 있다. 실험 데이터와 같은 객관적인 데이터는 의견, 생각등에 근거한 주관적인 데이터보다 훨씬
낫다.
Bayes 분석은 이용가능한 모든 데이터에 초기 신뢰도를 할당함으로써 시작한다.
초기 예측은 공학적 판단으로만 하거나 비슷한 종류의 아이템들로부터 얻은 데이터에 근거할 수도
있다. 그리고 나서, 추가적인 실험 데이터를 나중에 획득했을 때, 초기 신뢰도는 Bayes 정리을 적
용하여 수정된 신뢰도를 구할 수 있다. 이렇게 수정한 신뢰도는 ‘사후 신뢰도’라 불린다.
2. Bayes 정리 (Bayes' theorem)
Bayes 정리(Bayes theorem)는 새로운 정보에 의해 사상 B의 확률을 알 때, 이를 근거로 A가 발
생할 조건부 확률 P(A|B)를 구하는 방법론이다. 여기에서 새로운 정보가 주어지기 이전에 A가 발
생할 확률 P(A)를 사전확률(prior probability)이라 하고, 정보가 주어진 이후에 사상 A가 발생할 확
률 P(A|B)를 사후 확률(posterior probability)이라 한다.
사상 [그림 1]과 같이 A1, A2, … An은 모두 상호배반이며 이들을 모두 합하면 표본공간 S가 되는
표본공간의 분할사상이며, 사상 Aj가 발생할 확률은 P(Aj) ≠ 0 ( j = 1, 2, …, n )라고 가정한다.

조건부 확률의 정의에 따라서 P(An|B) = P(B∩An)/P(B)이며, P(B∩An) = P(B|An)P(An)이다.
그리고 A1, A2, … An는 표본공간 S의 분할사상이므로 사상 B가 발생하면 이 사상과 함께 분할사상
중 어느 하나는 반드시 발생하기 때문에 다음의 관계가 성립하는데, 이를 전확률공식이라 한다.
P(B) = P(B∩ A1) + P(B∩ A2) + … + P(B∩ An)
= P(B | A1) P(A1) + P(B | A2) P(A2) +… + P(B| An) P(An)
이상을 종합하면 조건부 확률 P(Aj|B)에 관한 다음의 관계식을 얻는데, 이를 Bayes 정리
(Bayes theorem)라고 한다.
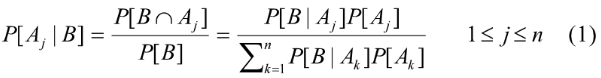
이는 Bayes 통계학에서 가장 기본적이며 유용한 이론이다. 이는 새로운 정보를 통해 사전확률을
수정하는 방법을 제시하고 있으나, 표본통계학자들은 사전확률을 주관적으로 부여한다는 점을
비판하고 있다. 그러나 간단한 일은 아니지만 사전확률을 정확히 알 수만 있다면, Bayes 통계학은
표본통계학의 경우보다 상대적으로 정확한 통계적 추론의 결과를 보여줄 수 있는 방법론이다. 이와
같은 Bayes 통계학을 이용하여 경험이나 직관에 의한 주관적 예측을 신뢰성 해석에 응용하여 정량
적으로 신뢰성을 평가하려는 것이 바로 Bayesian 신뢰성 해석(Bayesian reliability analysis)이다.
가. Bayes 예(이산 분포)
L 전자 회사는 TV생산의 주요 부품인 반도체를 A1, A2의 두 부품회사에서 공급받고 있다.
다음 표는 그 동안의 두 부품 회사의 제품에 대한 검사합격률을 나타낸 것이다.

여기서 G를 납품된 부품이 합격되는 사건, B를 납품된 부품이 불합격되는 사건이라 하면,
표에 의해서 다음과 같이 주어진다.
P(G|A1)=0.97, P(B|A1)=0.03
P(G|A2)=0.95, P(B|A2)=0.05
부품회사 A1과 A2 에서 납품받을 확률은 사전확률 P(A1)=0.6, P(A2)=0.4로서 주어진다고
하자. 표에서 주어진 조건부확률이 없을 경우, 누군가가 “불량품이 나왔는데 이것이 A1에서
제공되었을 확률을 묻는다면, A1에서 전체부품의 60%를 제공하므로 0.6이라고 대답할 수 밖
에 없다. 그러나 이제는 bayes 정리와 새로운 정보인 조건부 확률들을 이용하여 사후확률을
구할 수 있다. 불량품이 나왔을 때 이것이 A1에서 제공되었을 확률은 P(A1|B)로 표시될 수
있으며, 식(1)의 bayes 정리에 의해,

따라서,
P(A1|B)=(0.03*0.6)/(0.6*0.03+0.4*0.05)
=0.018/0.038≒0.47 이 된다.
즉, 불량품이 나왔을 경우 그것이 A1일 확률이 0.6에서 0.47로 바뀌게 되었다.
마찬가지로 불량품이 나왔을 경우 그것이 A2일 확률이 0.4에서 0.53로 바뀌게 되었다.
나. Bayes 예(연속 분포)
이산 분포의 예처럼, 기본식은 연속 확률 분포에서도 확장하여 사용할 수 있다. 예를 들면,
공학적 판단등과 같은 이전 테스트 결과를 전제로 하고, 이 테스트에서 시간 t동안 r이라는
고장이 관찰되었다고 하자. t에 대한 확률 밀도 함수는 감마 분포로써 다음과 같이 표현된다.

여기서
t는 테스트한 시간이다.(scale parameter)
r은 고장 횟수이다.(shape parameter)
또한
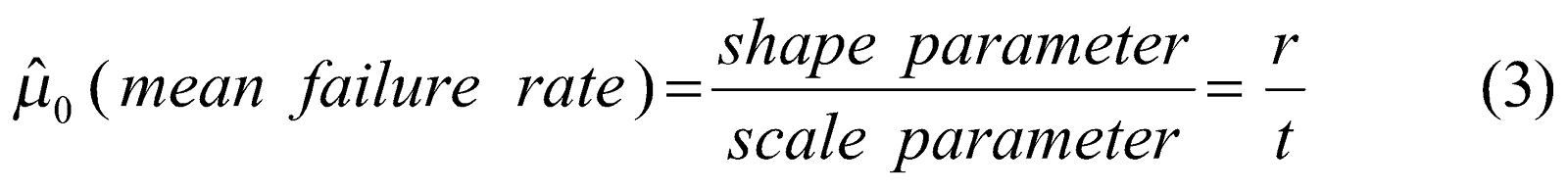
그리고

식 (3)과(4)는 사전 고장율과 사전 분산을 나타낸다. 각각의 값을 0.02와 (0.01)^2으로 가정
하자. t’=500 시간이고, r’=14 회라고 가정하자. ‘사후 고장율’ 값은 얼마인가?
연속 사후 분포에 대한 기본적인 표현은 다음식과 같다.

여기서,
f(λ)는 λ의 사전분포이다.식(2)이다.
f(t|λ)는 새로운 데이터에 근거한 t의 표본화된 분포이다.
f(t)는

f(λ|t)는 사전 분포와 새로운 데이터의 조합에 의한 사후 분포이다.
식(5)의 연산 수행의 결과로 새로 도출된 차후 분포는 다음 식으로 표현된다.

이식은 shape parameter = (r+r’), scale parameter = (t+t’) 의 또다른 감마 분포이다.
r과 t에 관하여 풀기 위해서 식(3)과(4)를 사용하면, 우리는 다음식을 얻는다.

그러므로,
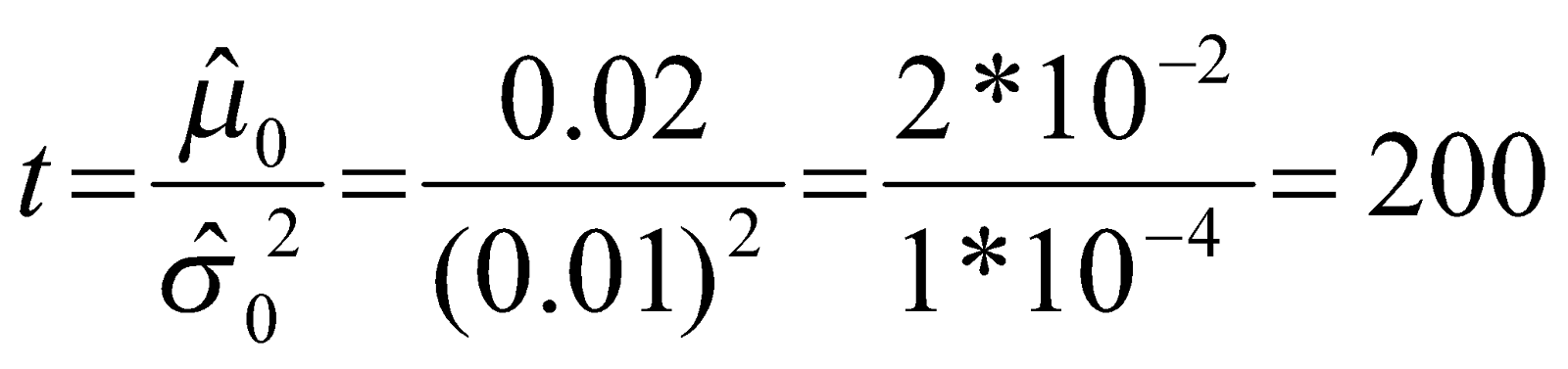

식(6)의 사후 감마 분포로 돌아가보면, 우리는 사후 고장율이 다음과 같음을 알 수 있다.
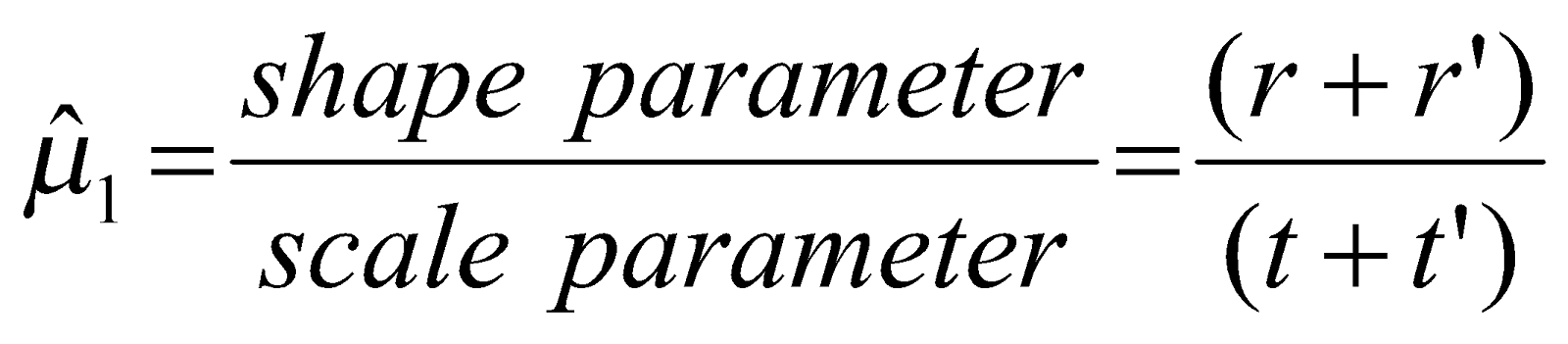
테스트 데이터인 r’=14, t’=500과 우리가 구한 r=4, t=200으로부터,

이 값을 테스트 결과로 얻어진 고장율 값인 14/500=0.028과 비교해 보자. 이전 정보의
사용으로 얻어진 고장율 값은 테스트 결과로 주어진 고장율 값보다 낮아짐을 알 수 있다.
참고 자료
- MIL-HDBK-338B “ELECTRONIC RELIABILITY DESIGN HANDBOOK”
- “ELEMENTS OF ENGINEERING PROBABILITY AND STATISTICS” Rodger E. Ziemer
- SR-332 “REALIBILITY PREDICTION PROCEDURE FOR ELECTRONIC EQUIPMENT”
(End)
'00 ILS Basics' 카테고리의 다른 글
| Reliability Metrics Convesion (0) | 2022.09.30 |
|---|---|
| DMSMS with PBL (0) | 2022.09.28 |
| Useful Site (2) | 2022.09.07 |
| 11대 요소 개발 (0) | 2022.09.05 |
| LSA Basics (1) | 2022.09.05 |




댓글