
A Study on the Calculation Method of Availability by Simulation
시뮬레이션을 이용한 가용도 산출 방안에 관한 연구
요약문
군 장비의 비용 효과적이고 효율적인 전투능력 달성을 위해 체계개발단계에서의 가용도 산출 방안을 시뮬레이션 사례를 통하여 제시하고 실제 무기체계의 가용도 산출에 도움이 되고자 한다.
I. 서론
가용도는 비용 최소화를 위한 무기체계의 핵심으로서 효과적인 체계와 적절한 지원이 이루어져야 한다. 그러므로 무기체계는 효과성과 지원성이 함께 설계되어야하며, 이러한 획득 과정은 비용 효과적이고 전투능력 요건을 달성하기 위한 필수적인 기반 지원을 제공해야 한다. 따라서 가용도의 이론적 배경을 검토하고 시뮬레이션 사례를 통해 체계 개발단계에서의 효과적인 가용도 산출에 도움이 되고자 한다.
II. 가용도
2.1 가용도 정의 및 종류
가용도는 어떤 주어진 시간에 있어서 장비가 작동상태에 있을 확률로서 임무가 요구된 어떤 시간에 장비의 임무수행 및 운용가능한 정도의 척도이다. 또한 장비의 전투준비태세를 평가해 주는 척도로서 운용환경에 따라 고유가용도, 성취가용도, 운용가용도 등으로 분류하며, 일반적인 개념의 가용도는 다음과 같다.

고유가용도(Ai:Inherent Availability)는 계획정비없이 규정된 조건하에서 가동상태에 있을 확률로서 장비자체 요인의 고장만을 반영한 것이다. 따라서 탐색 개발단계에서 장비의 설계개념을 설정할 때 이용한다.
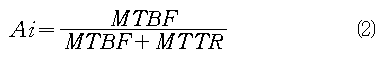
MTBF : Mean Time Between Failure
MTTR : Mean Time To Repair
성취가용도(Aa:Achieved Availability)는 고유가용도에 계획정비 시간을 추가로 고려한 것으로 장비자체의 직접적인 원인이 아닌 비가동 시간을 제외한 값이며, 이상적인 지원환경과 규정된 조건하에서 사용될 때 장비가 임의의 시점에서 작동할 확률로서 체계개발이 활발히 진행되는 선행개발단계로부터 최초 운용능력 확인단계까지 적용한다.

MTBM : Mean Time Between Maintenance
MAMDT : Mean Active Maintenance Downtime
운용가용도(Ao:Operational Availability)는 현실적으로 발생할 수 있는 모든 비가동 시간을 고려한 값으로 장비가 개발이 완료되어 야전에서 운용시 적용한다. 따라서 각 무기체계의 운용조건 및 여러 사항을 고려하여 체계에 알맞은 식을 도출하여야 한다.

MDT : Mean Downtime
2.2 System effectiveness 와의 관계
체계의 효율성을 위해 체계를 구성하는 중요한 요소들과 가용도와의 연관성을 그림 1에서 알 수 있다.
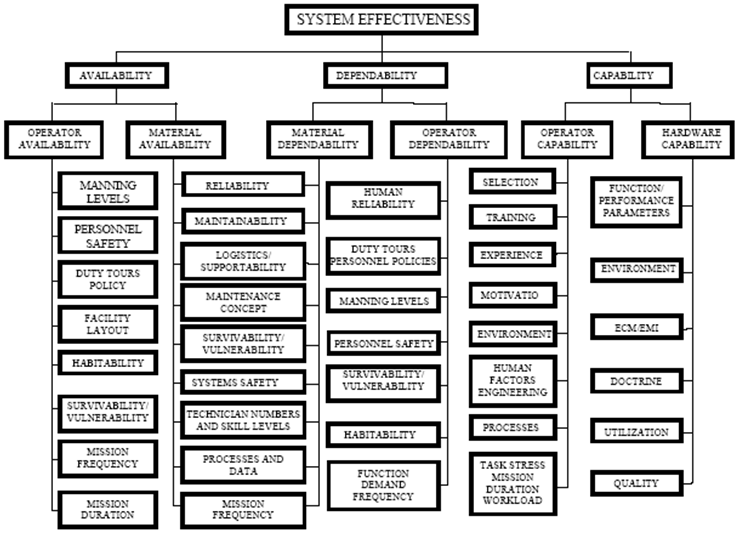
또한, 가용도의 여러 가지 요구사항들을 지원하기 위해 Cost-Benefit Tradeoff 분석을 수행하는데, 이 분석의 목적은 최소수명주기비용에서 명확하게 임무목적을 달성하기 위한 것이며, 대안 비교를 통해 계획과 관련된 가치를 평가하기 위한 기술이므로 과거의 결정을 평가할 때 유용하고, 최선의 방법을 선택할 때 매우 진보적인 사고를 할 수 있다. 특히, 운용가용도 계산 시 설계와 관련된 각 요소들과의 Tradeoff를 위한 기반을 마련하며, 임무의 효율성과 체계수명주기비용 평가에 용이하다.
III. 운용가용도 분석 사례
3.1 가정
1) 지원 및 시험장비는 분석 대상에서 제외하였다.
2) 가용도 분석은 체계 전체 및 장비 수준에서 산출하였다.
3) 신뢰도는 임무신뢰도로서 고장이 나더라도 장비의 기능이나 운용상에 영향을 미치지 않는 부품들의 고장율은 제외하였다.
4) 고유정비인수 IMF와 무결함 고장간 평균시간은 무시하였다. SO장비의 정비도 분석결과는 표 1과 같다.
5) SO장비의 고장율은 432.37회/106시간으로 산출되었다. 각 장치별 고장율 및 MTBF는 표 2와 같다.
표 1. SO 장비의 정비도 분석결과
| 항목 | 분석값 (시간) |
| MTTR | 1.16 |
| MTBPM | 24 |
| MAMDT | 1.008 |
| MTBM | 22.74 |
표 2. SO체계의 장치별 분석결과 1
| 품명 | 고장율 | MTBF | 업무빈도 | MTTR |
| SO체계 | 2312.81 | 432.37 | 10.15788223 | 1.16 |
| A | 34.98 | 28589.02 | 0.153625387 | 0.55 |
| B | 228.38 | 4378.72 | 1.003032519 | 0.82 |
| C | 228.38 | 4378.72 | 1.003032519 | 0.82 |
| D | 6.25 | 159887.06 | 0.02746939 | 0.28 |
| E | 43.54 | 22966.85 | 0.191232108 | 0.89 |
| F | 43.54 | 22966.85 | 0.191232108 | 0.89 |
| G | 43.11 | 23194.12 | 0.189358309 | 0.89 |
| H | 33.61 | 29751.60 | 0.147622295 | 2.32 |
| I | 9.58 | 104358.75 | 0.042085593 | 2.46 |
| J | 340.26 | 2938.95 | 1.494409573 | 0.29 |
| K | 48.78 | 20498.79 | 0.214256561 | 0.33 |
| L | 55.02 | 18174.86 | 0.241652455 | 0.26 |
| M | 37.31 | 26804.60 | 0.163852456 | 0.50 |
| N | 8.26 | 121074.47 | 0.036275195 | 0.50 |
| O | 162.99 | 6135.37 | 0.715849273 | 0.45 |
| P | 60.86 | 16430.27 | 0.267311539 | 0.56 |
| Q | 9.58 | 104358.75 | 0.042085593 | 2.46 |
| R | 454.19 | 2201.74 | 1.99478757 | 1.95 |
| S | 454.19 | 2201.74 | 1.99478757 | 1.95 |
| T | 6.82 | 146557.73 | 0.029967714 | 0.47 |
| U | 3.18 | 314691.87 | 0.013956509 | 0.50 |
표 3. SO체계의 장치별 분석결과 2
| 품명 | Ai | Aa | MTBM | MAMDT |
| SO체계 | 0.997 | 0.958 | 22.74 | 1.008 |
| A | 1.000 | 0.960 | 23.98 | 1.000 |
| B | 1.000 | 0.960 | 23.87 | 0.999 |
| C | 1.000 | 0.960 | 23.87 | 0.999 |
| D | 1.000 | 0.960 | 24.00 | 1.000 |
| E | 1.000 | 0.960 | 23.97 | 1.000 |
| F | 1.000 | 0.960 | 23.97 | 1.000 |
| G | 1.000 | 0.960 | 23.98 | 1.000 |
| H | 1.000 | 0.960 | 23.98 | 1.001 |
| I | 1.000 | 0.960 | 23.99 | 1.000 |
| J | 1.000 | 0.960 | 23.81 | 0.994 |
| K | 1.000 | 0.960 | 23.97 | 0.999 |
| L | 1.000 | 0.960 | 23.97 | 0.999 |
| M | 1.000 | 0.960 | 23.98 | 1.000 |
| N | 1.000 | 0.960 | 24.00 | 1.000 |
| O | 1.000 | 0.960 | 23.91 | 0.998 |
| P | 1.000 | 0.960 | 23.96 | 0.999 |
| Q | 1.000 | 0.960 | 23.99 | 1.000 |
| R | 0.999 | 0.959 | 23.74 | 1.010 |
| S | 0.999 | 0.959 | 23.74 | 1.010 |
| T | 1.000 | 0.960 | 24.00 | 1.000 |
| U | 1.000 | 0.960 | 24.00 | 1.000 |
3.2 SO장비의 운용가용도 산출과정
SO장비의 군수지연시간 ALDT를 72시간으로 가정하였을 때, 계산과정은 다음과 같다.
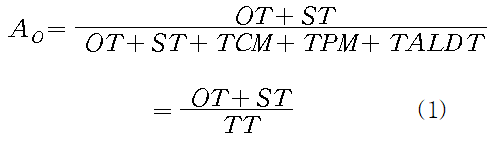
TT = 365 × 24 = 8760
OT = 4392
TCM = MTTR × OT / MTBF(비계획정비수)
= 1.16×4392/432.37 = 11.783
TPM = MTPM × OT /MTBPM(계획정비수)
= 1× 4392/24 = 183
ALDT = 72
TALDT = ALDT × OT / MTBF = 731.374
ST = TT - (OT + TCM + TPM + TALDT) = 3421.843
따라서,
Ao = (OT + ST) / TT
= (4392 + 3421.843) / 8760 = 0.894
TT : 총시간
OT : 운용시간
TCM : 총보수정비시간
TPM : 총예방정비시간
TALDT : 총 행정 및 군수지연시간
ST : 대기시간
IV. 시뮬레이션
4.1 개요
시뮬레이션이란 현실 문제를 반영하는 모형을 만들어 실험함으로서 현실 문제를 이해하고 여러 가지 대안의 결과를 예측하는 기법이다. 실제상황을 실험하기에는 비현실적이거나 위험요소가 크므로 현실에 적합한 모델을 사용하여 실험을 통해 미래상황을 예측해 볼 수 있다. 또한 시뮬레이션 모형의 다양한 모수들을 변화시킴에 따라 시뮬레이션 결과를 관찰하고, 다양한 환경하에서 실제상황이 어떠한 다른 상태로 전개될 것인지를 예측할 수 있다.
시뮬레이션을 사용하는 이유는 시스템이 복잡한 경우, 해석적인 해법이 없는 경우, 시스템 형태가 불규칙한 경우, 결과를 예측하기 어려운 경우에 다양한 변수들을 입력하여 결과를 예측하기 위해 사용하는 기법으로서 거시적인 분석에서부터 미시적인 분석에 이르기까지 유연하게 시스템을 모사할 수 있는 분석방법론이다. 따라서 문제를 해결하는데 있어 해석적방법이 불가능하거나 해석적 방법을 적용하기 위해서는 상당한 가정을 도입하여 문제를 간략화하는 것이 불가피한 경우에 주로 적용되며, 휴리스틱(Heuristic) 기법들 중의 하나로서 문제를 현시과 아주 가깝게 모형화할 수는 있니만 답을 찾는 데에는 모형의 복잡성 때문에 많은 시간과 어려움이 따르며 구해진 답이 최선이 아닐 수도 있다는 휴리스틱(Heuristic) 기법의 본래의 특징을 그대로 가지고 있다.
4.2 시뮬레이션의 장단점 및 유의사항
시뮬레이션의 장점은 첫째, 복잡한 현실 문제를 수리적인 방법으로 해결책을 구하지 못하는 경우에 유일한 해결책이다. 둘째, 시뮬레이션 모형으로 여러 가지 대안을 쉽게 비교할 수 있다. 셋째, 모형을 현실문제와 근접하게 만들 수 있으며, 이해 및 사용이 편리하여 문제 해결방법에 대해 의사결정자와 대화가 용이하다. 넷째, 장시간 경과 후에 결과를 알 수 있는 문제를 시뮬레이션하면 단시간에 결과를 예측할 수 있다.(시간단축 효과) 반대로 시간을 확장시켜 시뮬레이션을 할 수도 있다.(시간확장 효과)
시뮬레이션의 단점은 첫째, 시뮬레이션 모형개발에 많은 경험과 노력이 필요하다. 둘째, 확률적 시스템을 시뮬레이션할 때 관찰한 입력 자료를 사용해서 얻은 결과는 하나의 표본값에 해당한다. 따라서 여러 개의 표본값을 구하여 통계처리를 해야 하는 단점이 있으며 시간도 많이 소요된다.
시뮬레이션 기법을 사용하는 데에는 다음과 같은 유의사항이 있다. 첫째, 목표를 확실히 결정해야 한다. 둘째, 시뮬레이션 모형을 어느 정도 구체적으로 만들 것인가를 결정해야 한다. 셋째, 모형의 정확성을 항상 검토해야 한다. 넷째, 시뮬레이션 시작부터 끝까지 항상 의사결정자와 의견교환이 있어야 한다. 다섯째, 통계적 지식이 있는 사람이 참여해야 한다. 여섯째, 입력 자료가 정확해야 한다. 일곱째, 출력자료의 통계적 분석 시 자료의 독립성 여부를 고려해야 한다.
4.3 시뮬레이션 절차
어떠한 시스템에 대하여 시뮬레이션을 수행하는 절차는 상황에 따라서 달라질 수 있다. 하지만 대부분의 경우에는 시스템의 문제를 파악한 후 자료를 수집하여 모형을 만들고 모형의 정착성을 확인한 후 이 모형을 실행하고 결과를 분석하는 단계를 거치게 된다.
(1) 문제설정(Problem Formulation)
모든 시뮬레이션 분석은 분석대상 시스템에 대한 문제설정에서부터 시작된다. 이 단계는 시스템 관계자 또는 시뮬레이션 분석가에 의해서 수행되는데 만일 시뮬레이션 분석가가 시스템의 문제를 설정할 경우에는 그 결과를 반드시 시스템 관계자와 의논하여 올바른 문제설정이 이루어지도록 해야 한다.
(2) 분석목적 및 총괄계획수립(Setting of Objectives and Overall Project Plan)
이 단계에서는 시뮬레이션을 통하여 얻어내고자 하는 분석목적 및 어떻게 시뮬레이션 분석을 수행해나갈 것인가에 대한 총괄계획을 수립하게 된다. 어떤 종류의 분석이라도 마찬가지지만 시뮬레이션에서도 분석대상이 될 시스템과 분석목적 등을 초기에서부터 명확히 해 두어야 할 필요가 있다. 시스템은 그 분석목적에 따라 얼마든지 다르게 모형화하는 것이 가능하다.
(3) 모형구성(Model Building)
이 단계에서는 분석대상 실제 시스템을 수학적 구성요소와 그들간의 논리적 관계를 바탕으로 추상적인 개념모형(Conceptual Model)으로 변환시킨다. 모형구성 시 반드시 염두에 두어야 할 사항은 분석목적에 부합하는, 즉 필요로 하는 정보가 얻어지도록 필수적인 부분을 빠뜨리지 않도록 주의해야 한다는 점이다. 또한 모형을 만들어 나갈 때에는 해당 시스템을 처음에는 간단한 모형으로 표현한 후 점차 실제에 유사하도록 상세하게 발전시키는 상향접근법(Top-Down Approach)을 사용하는 것이 효과적이다.
(4) 자료수집(Data Collection)
시뮬레이션에 관련된 입력 자료의 조사 및 수집은 모형의 정확성 및 분석 결과에 절대적인 영향을 미치는 것인 만큼 충분한 기간에 걸친 충분한 양의 정확한 자료가 수집되어야 한다.
(5) 프로그램화(Coding)
이 단계에서는 (3)단계에서 만들어진 개념모형을 실제 프로그래밍 언어로 변환하는 작업을 수행한다. 프로그램 작성시 사용할 수 있는 언어로는 여러 가지가 있다. 일반목적언어(General Purpose Languag)인 FORTRAN, PASCAL, C, C++ 등을 쓸 수도 있고, 시뮬레이션 전용 언어인 GPSS, SLAM, SIMSCRIPT, SIMAN, MODSIM 등을 사용할 수도 있는데, 여러 가지 장점 때문에 시뮬레이션 전용언어의 사용이 적극 추천된다.
(6) 정확성검증(Verification)
정확성검증(Verification)은 (5)단계에서 작성된 컴퓨터 프로그램이 의도된 대로 만들어졌는지, 즉 (3)단계의 개념모형을 충실히 표현하고 있는가에 대한 입증작업이라고 할 수 있다. 이 작업은 시뮬레이션 모형이 복잡할수록 어려워지는데 가장 손쉬운 방법은 그 결과를 누구나 짐작할 수 있는 명백한 입력 자료를 넣어서 예상대로 답이 나오는지를 확인하는 것이다.
(7) 타당성 확인(Validation)
시뮬레이션 프로그램이 개념모형을 충실히 따르도록 작성(Coding)되었는지를 확인하는 정확성검증에 비해 타당성확인(Validation)은 이 프로그램의 바탕이 되는 개념모형이 시뮬레이션의 대상이 되는 실제 시스템을 정확하게 표현하고 있는가를 알아보는 것이다. 다시 말해 이 시뮬레이션 모형이 실제 시스템의 대체품으로 유효한지를 확인하는 것이다. 기존 시스템에서의 자료수집이 가능하다면 이를 모형의 결과 자료와 비교해 봄으로써 모형의 유효성을 평가해 볼 수 있고 자료수집이 불가능할 경우에는 다른 여러 기법들이 타당성확인을 위하여 사용된다. 만일 현 시뮬레이션 모형이 실제 시스템을 적절하게 표현하고 있지 못하다고 판단될 경우에는 (3)단계로 돌아가서 개념모형구성 부분을 다시 검토해야 한다.
(8) 실험설계(Experimental Design)
이 단계에서는 시뮬레이션 분석을 수행할 여러 가지 시나리오(Scenario) 또는 대안(Alternative) 각각에 대하여 시뮬레이션 수행 시간, 수행 횟수, 초기화 상태 등을 설정하게 된다.
(9) 시뮬레이션수행 및 결과분석(Production Runs and Analysis)
실험설계를 마친 각각의 시나리오 또는 대안들에 대한 실제 시뮬레이션 수행이 이 단계에서 이루어지며 그 결과는 각각의 시나리오의 실행척도(MOP, Measures Of Performance)를 도출해내기 위하여 사용된다.
(10) 추가분석여부 판단(More Runs)
시뮬레이션수행 및 결과분석단계에서 완료된 분석 결과를 바탕으로 하여 다른 시나리오나 추가적인 실행과정이 필요한지 결정한다.
(11) 문서화 및 결과보고(Documentation and Reporting)
시뮬레이션 모형자체 및 시뮬레이션 과정에 대하여 명확한 기록을 남기는 문서화는 차후 이 모형의 재사용 및 보완을 위하여 반드시 필요한 사항이다. 만약 현모형에 대한 설명 및 적용과정이 문서화되어 있지 않다면 제3자는 물론이고 그 모형을 구성하고 프로그램화 한 장본인일지라도 모형의 동작원리를 다시 파악하는데는 적지 않은 시간이 소요될 것이다. 이런데서 오는 시간 및 인력낭비는 철저하고도 명확한 문서화를 통하여 예방될 수 있으므로 이 부분에 미리 신경을 써야 한다.
시뮬레이션 분석결과의 보고는 명확하고도 간결하게 이루어져야 한다. 결과보고에는 현상황 분석, 대안들의 실행척도(MOP)비교를 통한 최적대안제시 등이 포함될 수 있다. 이 과정에서 명심해야 할 사항은 시뮬레이션을 수행할 때 바탕이 된 여리 가지 가정들 그리고 시뮬레이션 분석의 한계 등을 분석결과와 함께 보고함으로써 의사결정자가 단지 분석결과에만 너무 집착하지 않고 여러 가지를 종합하여 합리적인 판단을 내릴 있도록 유도해야 한다는 점이다.
(12) 실제 시스템에 적용(Implementation)
위의 모든 단계를 거쳐서 도출된 분석결과들을 바탕으로 최적 시나리오 또는 대안을 실제 시스템에 적용하는 단계이다.

V. 가용도 시뮬레이션 산출 예시
5.1 모형의 가정
(1) 일반적인 운용가용도 산출식을 적용한다.
(2) MTBM 은 지수분포를 따르며, 평균 120시간이다.
(3) MDT는 대수정규분포를 따르며, 평균 4시간, 표준편차가 1시간이다.
(4) 시뮬레이션은 100번을 반복하여 실행한다.
(5) 시뮬레이션 모형은 동적, 확률적, 이산적 모형을 기반으로 한다.
5.2 시뮬레이션 수행 결과
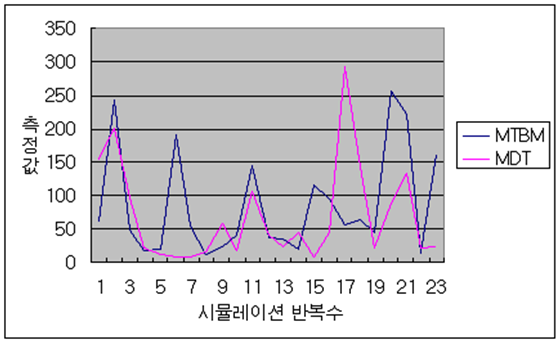
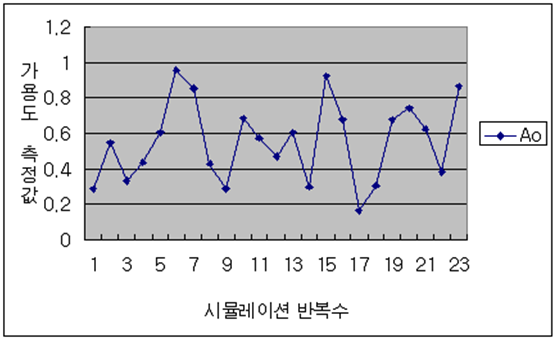
시뮬레이션을 수행 후 결과값은 다음과 같다.
표 4. 가용도 시뮬레이션 측정값
| 반복수 | MTBM | MDT | Ao |
| 1 | 62.71962385 | 153.4882276 | 0.290089483 |
| 2 | 243.3763178 | 201.7515567 | 0.546755959 |
| 3 | 48.58278847 | 96.83321694 | 0.334095194 |
| 4 | 16.69732987 | 21.26917642 | 0.439791055 |
| 5 | 18.67500761 | 12.01267042 | 0.608550689 |
| 6 | 189.9602694 | 8.306111423 | 0.958106304 |
| 7 | 53.75506427 | 9.202798401 | 0.853826067 |
| 8 | 11.28198574 | 15.03337725 | 0.428722406 |
| 9 | 23.61729179 | 58.18848812 | 0.288699549 |
| 10 | 39.92193567 | 18.11769619 | 0.68783923 |
| 20 | 142.9791121 | 104.9544204 | 0.576683237 |
| 50 | 35.77629636 | 40.64931563 | 0.4681192 |
| 90 | 34.27435243 | 22.01444672 | 0.608901823 |
| 100 | 161.2881267 | 24.69831427 | 0.867203684 |
표 5. 가용도 측정값 구분
| 구분 | MTBM | MDT | Ao |
| 평균 | 113.0851211 | 84.10916829 | 0.543319558 |
| 중간 | 71.57131706 | 59.31141685 | 0.608726256 |
| 최대 | 296.6479518 | 5.458647268 | 0.981931387 |
| 최소 | 2.153403758 | 205.126187 | 0.010388885 |
VI. 결론
본 논문은 시뮬레이션을 통한 가용도 산출에 필요한 이론적 배경과 사례를 제시하여 향후 최적 가용도를 판단하는데 도움을 주고자 하였다. 실제 무기체계의 가용도 산출에 적용하기 위해서 시뮬레이션 각 단계에 적합한 자료를 수집하고 통계적 자료분석과 시뮬레이션 수행 및 검증을 통해 가용도와 Cost-Benefit Tradeoff의 상관관계도 고려한다면 보다 효율적인 무기체계 개발에 도움이 될 것이다.
참고문헌
[1] 하형호, “군 기동장비 가용도 분석을 통한 교체시기 결정에 관한 연구,”석사학위 눈문, 국방대학교, 2003.
[2] 남흥국, “ARENA를 이용한 해군 함대 정비인력 및 전투함 가용도 상관관계 분석에 관한 연구,” 석사학위 논문, 국방대학교, 2001.
[3] Christopher A. Chung, "Simulation Modeling Handbook," CRC PRESS, 2004
[4] Joel Manary, "Operational Availability Handbook," RAC, 2004.
[5] W.David Kelton, Randall P. Sadowski, Deborah A. Sadowski, "Simulation With ARENA, 2E," Mc Graw Hill, 2002.
[6] 김재련, “컴퓨터시뮬레이션,” 박영사, 2000.
[7] 이영해, 백두권, “시스템 시뮬레이션,” 경문사, 1994.
(End)
'03 LSA & PSA' 카테고리의 다른 글
| System Operational Effectiveness Measurement Model at Logistics Support (0) | 2022.10.31 |
|---|---|
| NAVAIR 00-25-403, The Naval Aviation RCM Process (0) | 2022.10.28 |
| NASA Technical Memorandum 4628A, DFE (0) | 2022.10.28 |
| MIL-STD-1388-2B, APPENDIX B “Logistic Support Analysis Record Report” (0) | 2022.10.28 |
| FMEA Specifications Review (0) | 2022.10.24 |




댓글